PC Painter and MM Coleman
Fundamentals of Polymer Science
(2nd Edition, CRC Press)

Chapter 7

Concepts that you must know:
  1. Review -also from previous courses material- the following: phase transition, first order phase transition, types of intermolecular interactions (van der Walls, electrostatic, dipole-dipole, hydrogen bonding)
  2. Bond rotations, bond rotation potential, trans / gauche for sp3 carbon.
  3. Crystalline materials and X-Ray Diffraction. Crystal unit cell for small molecules and polymers. Polymeric crystals: fringed micelles, spherulites, chain folds, tie molecules.
  4. Polymer crystals from solution, from the melt, shear-induced.
Exercises:
  1. * Go through the 'random walk' derivations of 7.D, esp. the relations on the mean square end-to-end distance (eq. 7.14) and the associated probability distribution P(R) or W(R) (eq. 7.23, fig. 7.14).
  2. * Explain rubber elasticity based on the concept of end-to-end probability distribution W(R).
  3. * Go through study question 5 (pg. 256), esp. on how mechanical properties and optical transparency depend on the polymer state.
Interactive Module:
The interactive module below is an Adobe Flash object (whose native support is deprecated); you will need a Flash Emulator extension for your browser: there are several available for free in your browser's extension/web store (we recommend the "Ruffle Flash Emulator" extension, also "Flash Player Emulator 2024", "Flash works Again" and "Flash Player Enabler" seem to be as good for this course's interactive modules).


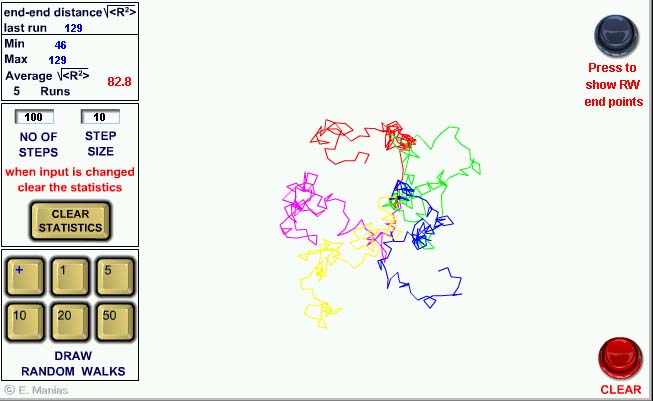
  1. Start by a 1 step RW (set the step to a large number, e.g. 90) and plot 150 RWs. Notice how the ends are arranged.
    Change to 2 steps and comment on how the distribution of ends changes. How many runs do you need to start approaching the statistical average of the mean square end-to-end ?
  2. Make 900 RW of 2 steps and comment on the existence of RWs that end near the starting point (i.e. end-to-end close to zero)
  3. Choose 100 steps of RW (set the step to a small number, e.g. 10) and make 10, 20, 30, ..., 100 RWs. Comment on the RW end distribution and the running mean square end-to-end average.
  4. Choose a small step length (e.g. 5) and make increasingly longer RWs: 10, 20, 100, 200, ..., 999. Is RW an effective trajecory to get away from the starting point? Comment on how your qualitative observation can be quantified through the average mean square end-to-end distance.